Search
Search Problems
- Maze => Driving Directions
- 15 Sliding Tiles
Terminologies
Agent
- An entity that perceives its environment and acts upon that environment.
State
- A configuration of the agent and its environment.
- For eg, in a 15 sliding tile example, the initial position of the tiles can be the state.
Initial State
- The state from where the agent begins.
Actions
- Choices that can be made in a state.
- Actions(s) returns the set of actions that can be executed in a state s.
- "Actions(s)" is a function which takes 's' parameter which can be the initial state of a problem.
- It returns as output the set of actions that can be executed.
Transition Model
- A description of what state results from performing any applicable action in any state.
- Result(s, a) returns the state resulting from performing action a in state s.
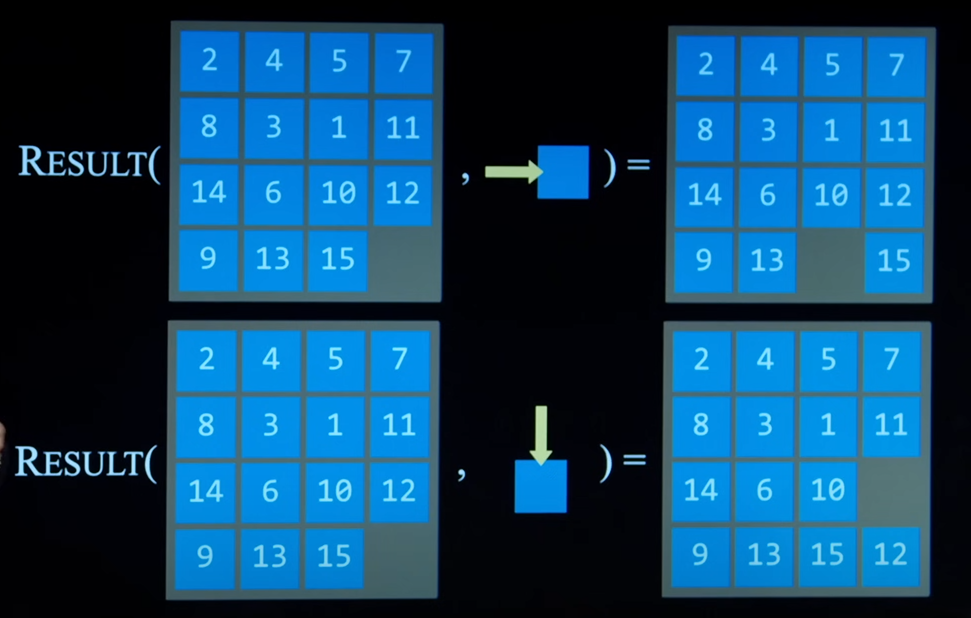
State Space
- The set of all the states reachable from the initial state by any sequence of actions.
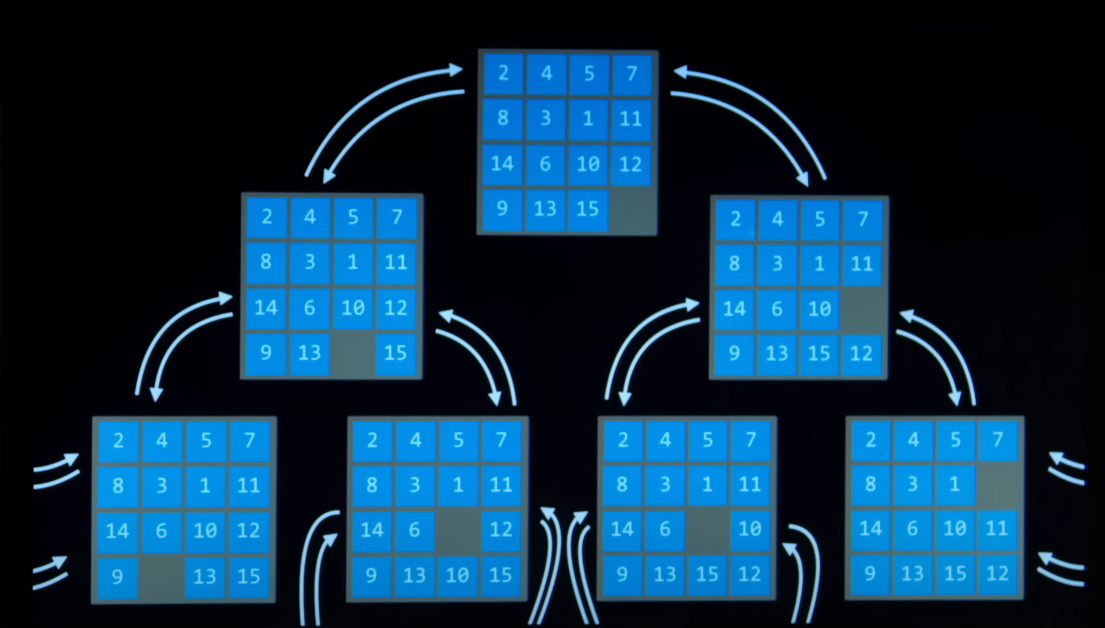
Simplified Representation as graph
Goal Test
- A way to determine whether a given state is a goal state.
Path Cost
- Numerical cost associated with a given path.
Solution
- A sequence of actions that leads from the initial state to a goal state.
Optimal Solution
- A solution that has the lowest path cost among all solutions.
Now we need to begin to figure out that how is it that we are going to solve this kind of search problem. To do that our computer needs to represent a whole bunch of data about the problem. Often times when we are packaging the whole bunch of data, related to a state, together, we will do so using a data structure, that we are going to call a Node.
Node
- A data structure that keeps track of - A state - A parent (node that generated this node) - An action (action applied to parent to get current node) - A path cost (from initial state to current node) From a given state, we have multiple options to take. We are going to explore those options. Once we explore those options, we will find that more options than that are going to make themselves available. We are going to consider all of the available options to be stored inside a single data structure that we will call the frontier.
Approach
- State with a frontier that contains the initial state.
- Repeat
- If frontier is empty, then there is no solution.
- Remove a node from the frontier.
- If the node contains the goal state, return the solution.
- Expand node, adding resulting nodes to the frontier.
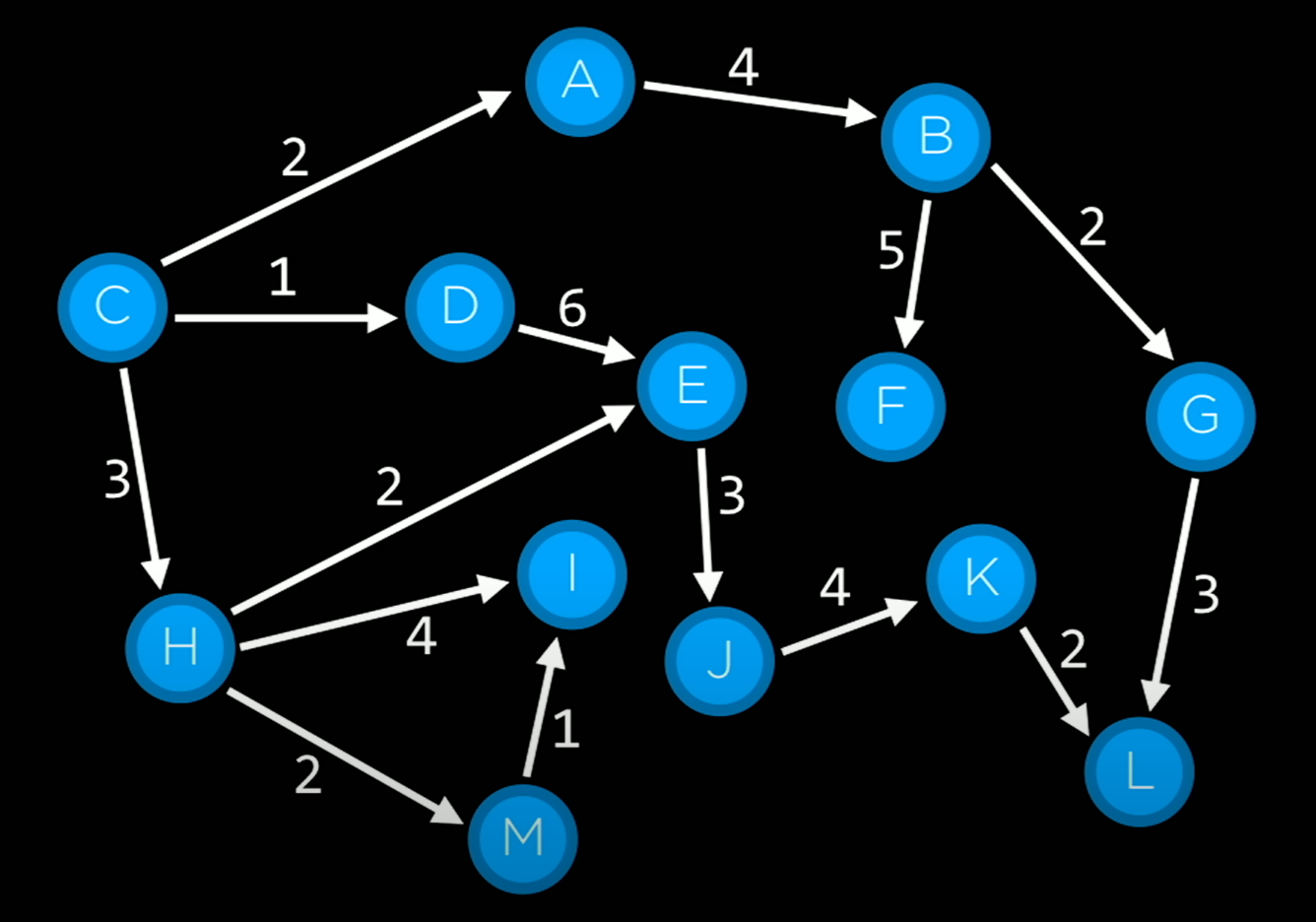
Example
- Find a path from A to E.
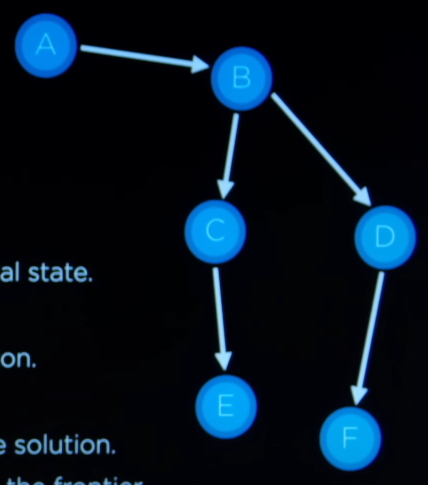
Frontier = A
Step 1: Remove the node from frontier
Step 2: A is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = B.
Frontier = B
Step 1: Remove the node from frontier
Step 2: B is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = C, D.
Frontier = C, D
Step 1: Remove the node C from the frontier.
Step 2: C is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = E, D.
Frontier = E, D
Step 1: Remove the node E from the frontier.
Step 2: E is the goal state. Hence, return the solution.
- Find a path from A to E.
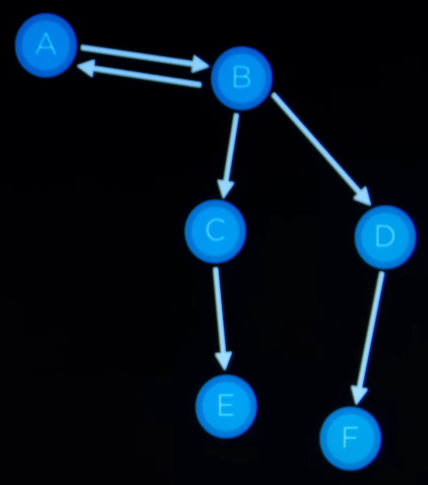
Frontier = A
Step 1: Remove the node from frontier
Step 2: A is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = B.
Frontier = B
Step 1: Remove the node from frontier
Step 2: B is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = A, C, D.
Frontier = A, C, D
Step 1: Remove the node A from the frontier.
Step 2: A is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = B, C, D.
Frontier = B, C, D
Step 1: Remove the node from frontier
Step 2: B is not the goal state.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = A, C, D.
This can get into an infinite loop since it keeps going back and frontend between the two states. The solution to this problem is to keep track of already visited node. Once the state is explored, dont bother to add it back to the frontier.
Revised Approach
- Start with a frontier that contains the initial state.
- Start with an empty explored set.
- Repeat: - If the frontier is empty, there is no solution. - Remove a node from the frontier. - If the node contains the goal state, return the solution. - Add the node to the explored state. - Expand node, adding the resulting node to the frontier, if that node is not already in the frontier or explored yet. The frontier is a data structure. The order in which we remove the node will be that of a stack, that is, last in first out.
Example
- Find a path from A to E.

Frontier = A
Step 1: Remove the node from frontier.
Step 2: A is not the goal state.
Step 3: Add A in the Explored Set, that is, Explored Set = A.
Step 4: Expand node, adding resulting nodes to the frontier, that is, Frontier = B.
Frontier = B
Step 1: Remove the node from frontier
Step 2: B is not the goal state.
Step 3: Add B in the Explored Set, that is, Explored Set = A, B.
Step 4: Expand node, adding resulting nodes to the frontier, that is, Frontier = C, D.
Frontier = C, D
Step 1: Remove the node D from the frontier. // Removing D and not C because we are following stack approach, that is, last in first out.
Step 2: D is not the goal state.
Step 3: Add D in the Explored Set, that is, Explored Set = A, B, D.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = C, F.
Frontier = C, F
Step 1: Remove the node F from the frontier.
Step 2: F is not the goal state.
Step 3: Add F in the Explored Set, that is, Explored Set = A, B, D, F.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = C.
Frontier = C
Step 1: Remove the node C from the frontier.
Step 2: C is not the goal state.
Step 3: Add C in the Explored Set, that is, Explored Set = A, B, D, F, C.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = E.
Frontier = E
Step 1: Remove the node E from the frontier.
Step 2: E is the goal state. Hence, return the solution.
When we use Stack approach, when watching visually, we first go deep on one side and then explore the other side. We first go from A -> B -> D -> F -> C -> E. This type of search is called as Depth-First Search.
Depth-First Search (DFS)
- Search algorithm that always expands the deepest node in the frontier.
- We use Stack data structure for the depth first search. It follows last in first out approach.
Breadth-First Search (BFS)
- Search algorithm that always expands the shallowest node in the frontier.
- We use Queue data structure for the depth first search. It follows first in first out approach.
Example
- Find a path from A to E.

Frontier = A
Step 1: Remove the node from frontier.
Step 2: A is not the goal state.
Step 3: Add A in the Explored Set, that is, Explored Set = A.
Step 4: Expand node, adding resulting nodes to the frontier, that is, Frontier = B.
Frontier = B
Step 1: Remove the node from frontier
Step 2: B is not the goal state.
Step 3: Add B in the Explored Set, that is, Explored Set = A, B.
Step 4: Expand node, adding resulting nodes to the frontier, that is, Frontier = C, D.
Frontier = C, D
Step 1: Remove the node C from the frontier. // Removing C and not D because we are following queue approach, that is, first in first out.
Step 2: C is not the goal state.
Step 3: Add C in the Explored Set, that is, Explored Set = A, B, C.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = D, E.
Frontier = D, E
Step 1: Remove the node D from the frontier.
Step 2: D is not the goal state.
Step 3: Add D in the Explored Set, that is, Explored Set = A, B, C, D.
Step 3: Expand node, adding resulting nodes to the frontier, that is, Frontier = E, F.
Frontier = E, F
Step 1: Remove the node E from the frontier.
Step 2: E is the goal state. Hence, return the solution.
Maze Problem
Depth-First Search
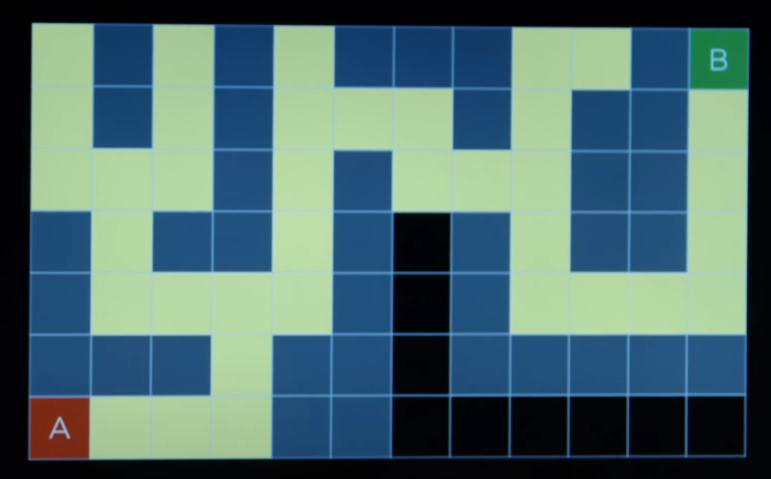
- As long as our maze is finite, DFS is going to find a solution.
- DFS does not necessarily will be the optimal solution. For example, in the following maze, there are multiple solutions. If it chooses the right direction in the first turn, it reaches the goal faster; however, there is not a particular reason for the DFS to choose that first. Alternatively, DFS can choose the other path and make the solution much longer.
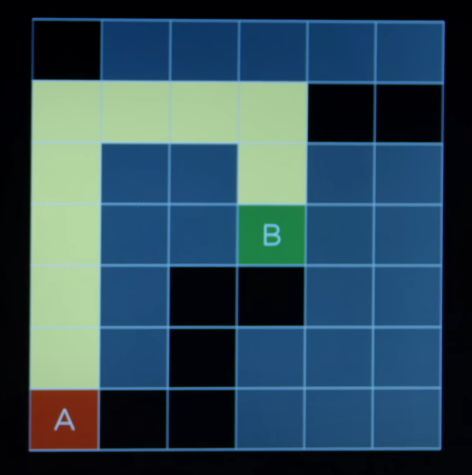
Breadth-First Search
- BFS takes the approach of exploring all the possible paths at the same time. It takes on step on all the sides.
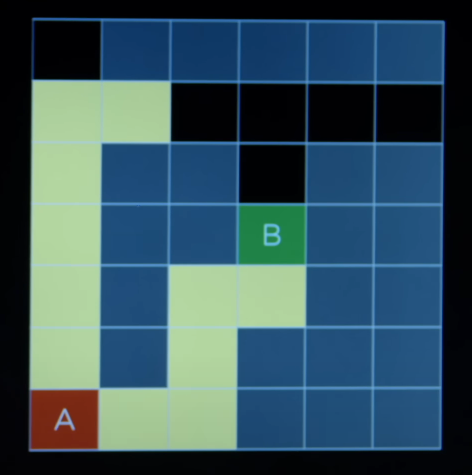
- Although in this case, we need to explore some paths that does not takes us anywhere, the path that we found to the goal, was the optimal path, that is, the shortest way, we can get to the goal.
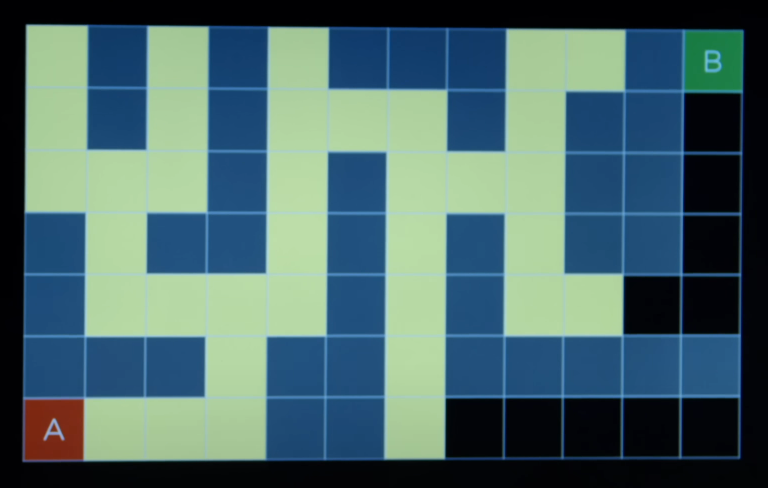
- When looking at the bigger maze, although the BFS finds the optimal solution, the trade off is that, it needs to explore a lot of state before reaching the goal.
Uninformed Search
- Search strategies that uses no problem-specific knowledge.
- For eg, DFS and BFS.
Informed Search
- Search strategy that uses problem-specific knowledge to find solutions more efficiently.
- There are number of different types of informed search.
Greedy Best-First Search
- Instead of exploring the deepest node (DFS) or the shallowest node (BFS), GBFS is always going to explore the node that it thinks is the closest to the goal state.
- However, it does not always know, which node is the closest to the goal, we can use the estimate of whats the closest to the node. We do this by using an heuristic function h(n).
- It takes the status input and returns an estimate of how close we are to the goal.
Heuristic function in case of the maze:
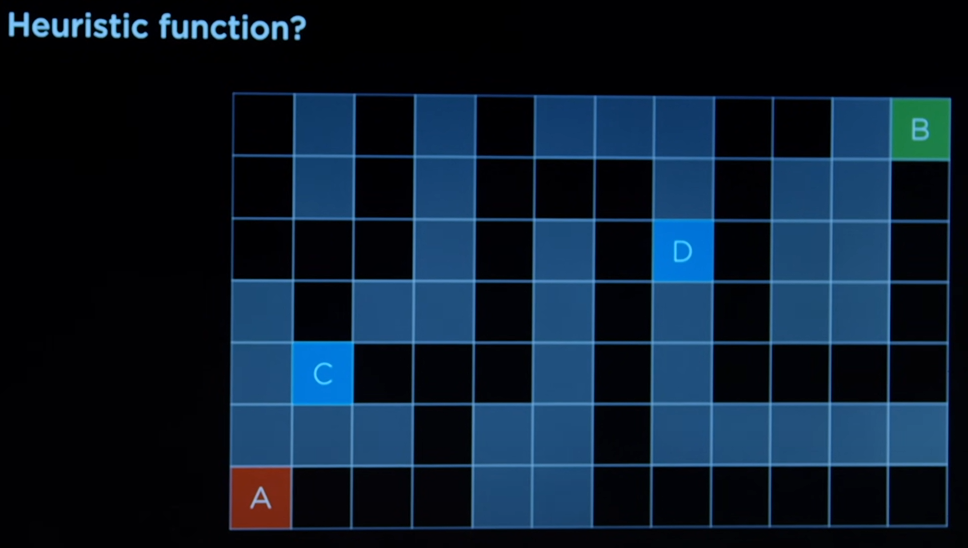
- The heuristic needs to estimate between the two cells, that is C and D, which one is the better to reach the goal.
- ignoring the walls, geographically, D seems to be the better place.
Manhattan Distance
- This is the heuristic function that we are going to use.
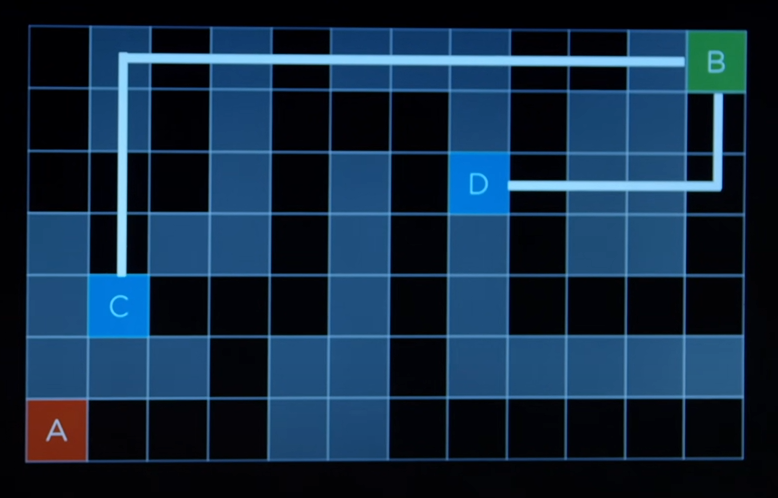
- Only allowing to go vertically or horizontally, how many steps are required from each points to reach the goal state.
- It turns out the D is much closer to the goal and needs to take less steps than C.
Approach
- Remove the node from the frontier.
- Explore the node, if it has the smallest value / the smallest Manhattan distance to the goal.
Each cells marked with the Manhattan distance to the goal
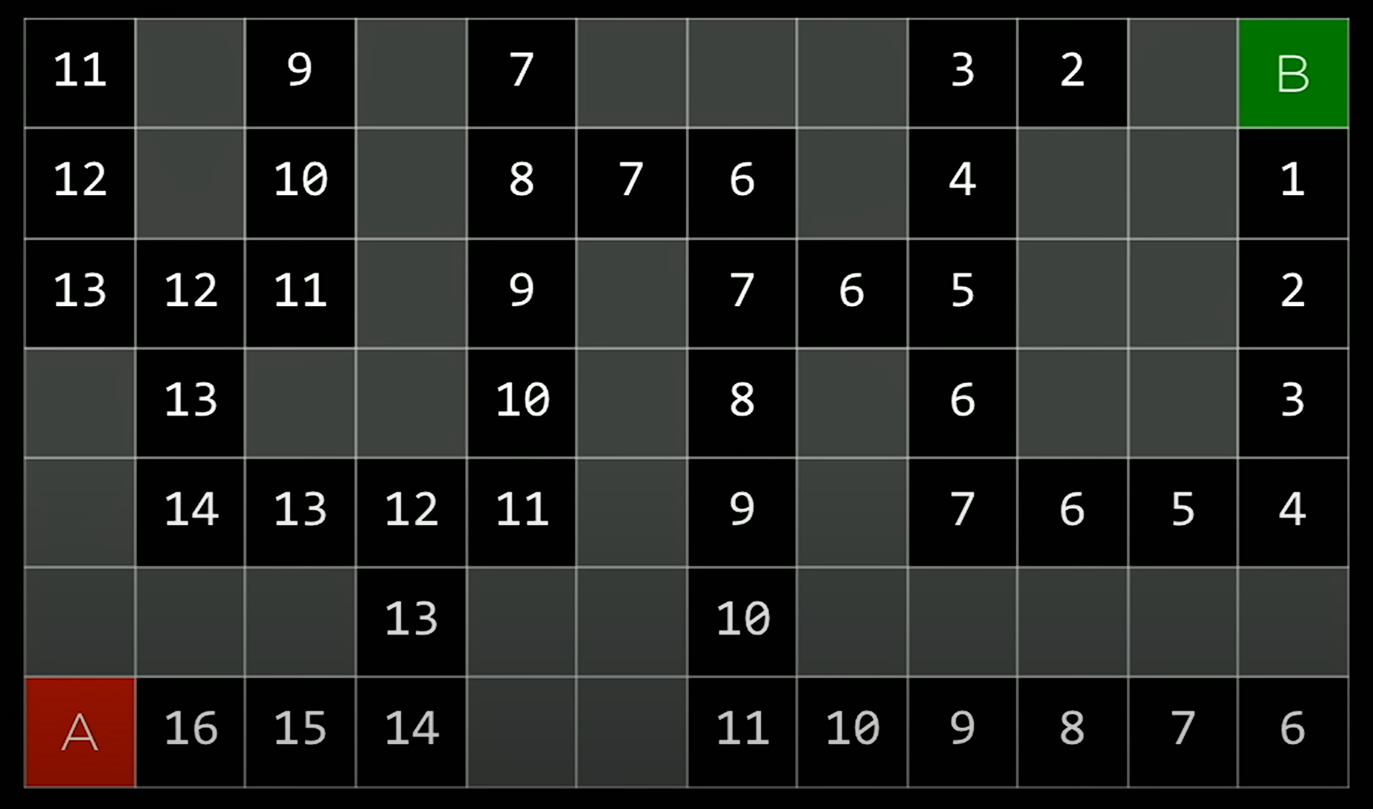
- Now, when there is a choice, we can pick up to go to the cell that is more closer to the goal.
- This time the algorithm makes an informed decision.

- Now, we need to come up with a good heuristic.
- Coming up with a good heuristic, can often time be more challenging.
- Considering the following maze, GBFS algorithm with find the following path to the goal state.
- However, the other path is the shortest to the goal state.
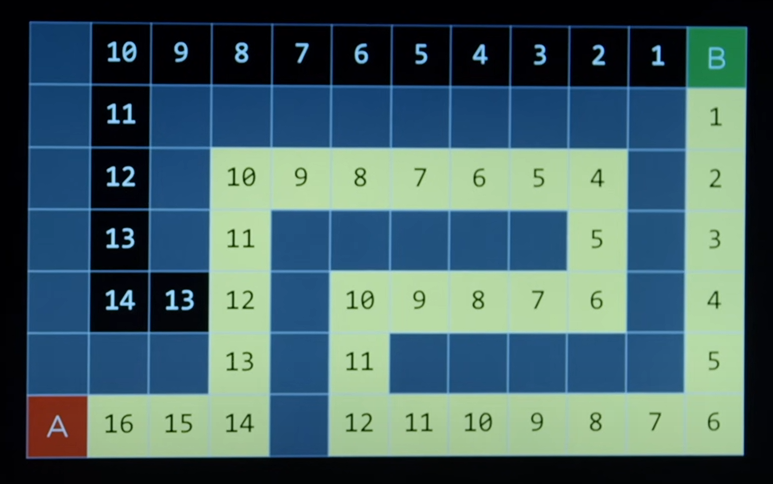
- The reason why this solution was not great is that, yes the heuristic numbers went down quickly, but they increase again quickly.
- Alternatively, we could have taken a fewer steps by going to the 13 instead of 11 to reach to the goal state.
- Well, 13 big then 11 so it does not looks like a good choice, but it requires far fewer steps.
- It requires less steps to reach 13 from the initial state then to reach 12 from the initial state.
- Hence, the algorithm would rather choose to go to 13 which looks heuristically longer; but I can reach there quickly.
- We are going to code this idea in a form of general algorithm known as A* search.
A* Search
- Search algorithm that expands node with the lowest value of g(n) + h(n).
g(n) = cost of reach node h(n) = estimated cost to goal
- The greedy best first search algorithm will only care about the heuristic distance between the current state to the goal, whereas, A* search will take into consideration, two pieces of information, how far the estimate is the current state from the goal, and also how far did the current state have to travel to get there because that is relevant too.
- Following is how the A* Search algorithm will move considering the sum of both the pieces of information.
- The final solution that this algorithm finds will be the optimal solution to reach to the goal.
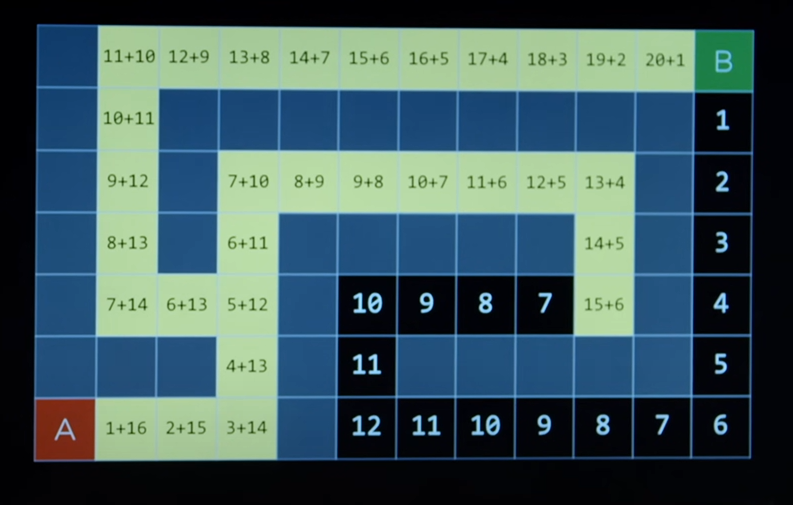
- A* Search is an optimal search algorithm, considering the following conditions:
- h(n) is admissible. Never overestimates the true cost. It either needs to always be right of how far it is from the goal state or it needs to underestimate.
- h(n) is consistent. For every node n and successor n' with step cost c,
h(n) <= h(n') + c.
Minimax
- MAX aims to maximize score.
- MIN aims to minimize score.
Game
- S0: Initial State
- Player(s): Returns which player to move in state s
- Actions(s): Returns legal moves in state s
- Result(s, a): Returns state after action a taken in state s.
- Terminal(s): Checks if state s is a terminal state.
- Utility(s): Final numerical value for terminal state s.
Initial State

Player(s)
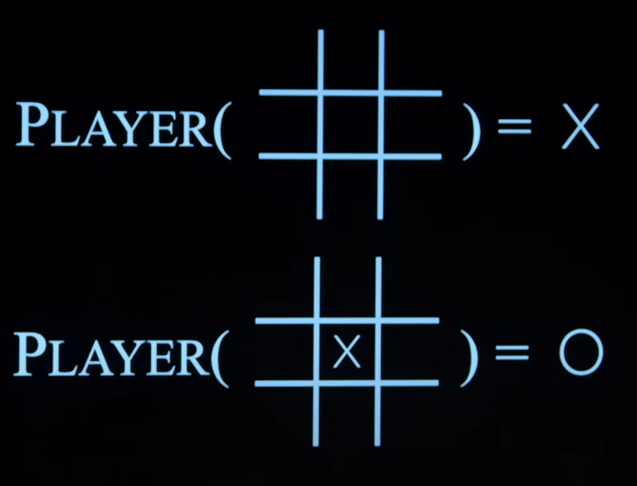
- If the game board is empty, the player function is going to return the function will return X.
- If the game board where X had made a move, the function is going to return O.
Actions(s)
- Takes a state and returns a set of all the possible actions that can be taken from that state.
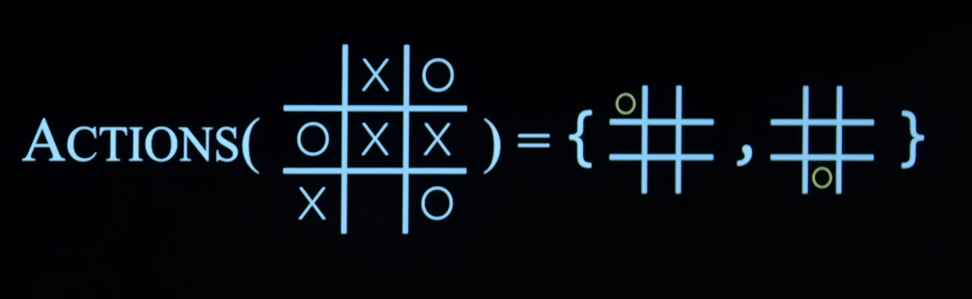
Result(s, a)
- When we get state and actions, we need a transition model to tell us when we take the action on a state, what is the new state that we get.
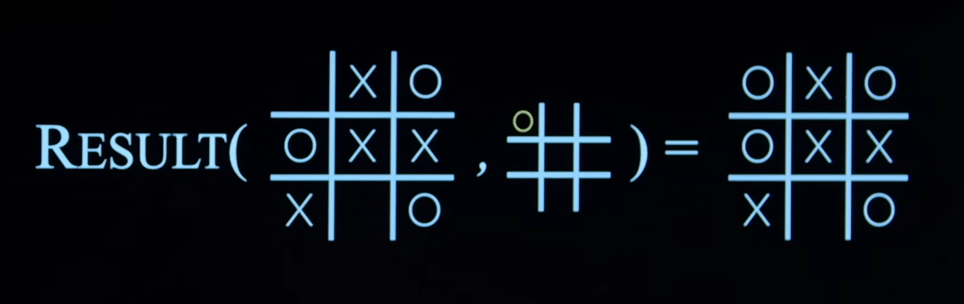
Terminal(s)
- The AI needs to know how the game works and the AI needs to know when the game is over.
- This terminal function informs AI if the game is over.
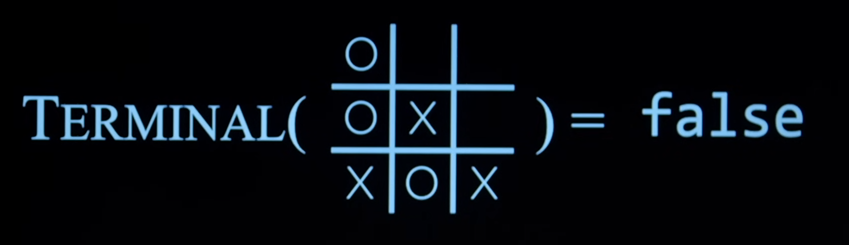
Utility(s)
- It takes the state s and returns the score or the utility of that state.
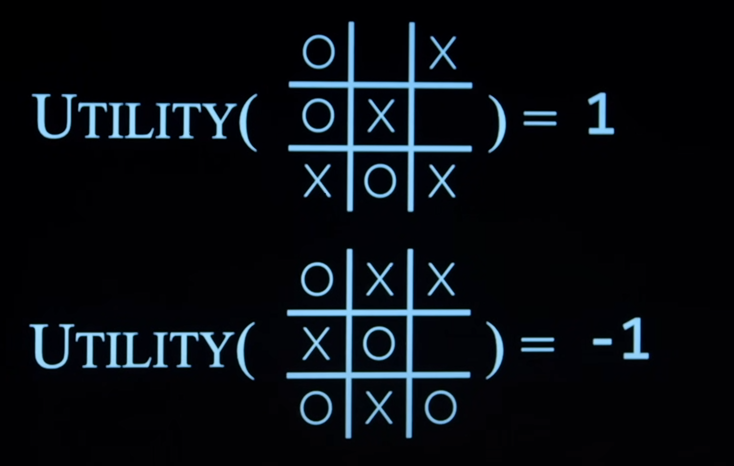
Minimax
- Given a state s:
- MAX picks action a in Actions(s) that produces highest value of Min-Value(Result(s, a)).
- MIN picks action a in Actions(s) that produces smallest value of Max-Value(Result(s, a)).
Max-Value(state)
- It takes a state and returns as a output the value of that state if I am trying to maximize the value of the state.
function Max-Value(state):
if Terminal(state): return Utility(state)
# The value initially needs to be as low as possible becaue as I consider my actions, I am always going to try and do better than v. And if the v is set of negative infinity, it can only go better than that.
v = -∞
# For every action in the actions of state; where Actions is the function which takes the state and return all the actions that can be taken from that state.
for action in Actions(state):
# Result(state, action) takes the current state and action and returns the value of the resulting state when the passed action is performed on the past state.
# Min-Value(Resulting State Value) returns the value of the next action that the opponent will take after the resulting state.
# Max(v, Value of next action that the opponent will take.) returns the maximum value between the two values.
v = Max(v, Min-Value(Result(state, action)))
return v
Mini-Value(state)
- It takes a state and returns as a output the value of that state if I am trying to minimize the value of the state.
function Min-Value(state):
if Terminal(state): return Utility(state)
# The value initially needs to be as high as possible becaue as I consider my actions, I am always going to try and do lesser than v. And if the v is set of infinity, it can only go lesser than that.
v = ∞
# For every action in the actions of state; where Actions is the function which takes the state and return all the actions that can be taken from that state.
for action in Actions(state):
# Result(state, action) takes the current state and action and returns the value of the resulting state when the passed action is performed on the past state.
# Max-Value(Resulting State Value) returns the value of the next action that the opponent will take after the resulting state.
# Min(v, Value of next action that the opponent will take.) returns the maximum value between the two values.
v = Min(v, Max-Value(Result(state, action)))
return v
Using these functions, we recursively call max-value and min-value until we reach the terminal state where we return the utility of that terminal state. This is a whole long process especially when the game becomes complex with more moves and more options.